排序算法
排序算法评价维度
运行效率:时间复杂度、总体操作数
就地性:原地排序在原数组上直接操作实现排序,无需借助额外的辅助空间,节省内存。通常,原地排序的数据搬运操作少,运行速度也更快。
稳定性:稳定排序在完成排序后,相等元素在数组中的相对顺序不变。
自适应性:自适应排序的时间复杂度会受到输入数据的影响,即最佳时间复杂度、最差时间复杂度、平均时间复杂度并不完全相等。
是否基于比较:基于比较的排序依赖比较运算符(
>,=,<)来判断元素的相对顺序,从而排序整个数组理论最优时间复杂度为O(nlogn)。而非比较排序不使用比较运算符,时间复杂度可达O(n),但其通用性相对较差。
选择排序
循环,每轮从未排序区间选择最小的元素,放到已排序区间的末尾
def select_sort(nums:list[int]):
n=len(nums)
# 外循环:未排序区间[i,n-1]
for i in range(n-1):
# 内循环:寻找最小元素
k=i
for j in range(i+1,n):
if nums[j]<nums[k]:
k=j
nums[i],nums[k]=nums[k],nums[i]特性
时间复杂度
O(n平方)、非自适应性排序空间复杂度
O(1)、原地排序非稳定性排序
冒泡排序
连续比较与交换相邻元素实现排序
如果"左元素 > 右元素"就交换,最终最大元素被移动到最右端
def bubble_sort(nums:list[int]):
n=len(nums)
# 外循环: [0,i]
for i in range(n-1,0,-1):
# 内循环:把未排序区间中的最大元素交换到最右端
for j in range(i):
if nums[j]>nums[j+1]:
nums[j],nums[j+1]=nums[j+1],nums[j]优化
如果某一轮冒泡没有执行交换操作,说明已完成排序
def bubble_sort_with_flag(nums:list[int]):
n=len(nums)
# 外循环:未排序区间 [0,i]
for i in range(n-1,0,-1):
flag=False
# 内循环:把未排序区间中的最大元素交换到最右端
for j in range(i):
if nums[j]>nums[j+1]:
nums[j],nums[j+1]=nums[j+1],nums[j]
flag=True
if not flag:
break特性
时间复杂度
O(n平方)、自适应排序空间复杂度
O(1)、原地排序稳定排序
插入排序
在未排序区间选择一个基准元素,将该元素与其左侧已排序区间的元素逐一比较大小,并将该元素插入到正确的位置
def insertion_sort(nums:list[int]):
# 外循环:已排序区间为[0, i-1]
for i in range(1,len(nums)):
# 基准元素
base=nums[i]
j=i-1
# 内循环:将base插入已排序区间[0,i-1]中的正确位置
while j>=0 and nums[j]>base:
nums[j+1]=nums[j] # nums[j]向右移
j-=1
nums[j+1]=base # 将base放置到正确位置特性
时间复杂度
O(n平方)、自适应排序空间复杂度
O(1)、原地排序稳定排序
优势
快速排序时间复杂度O(nlogn),虽然插入排序时间复杂度更改,但在数据量较小的情况下,插入排序通常更快
快速排序
是一种基于分治策略的排序算法,运行高效,应用广泛
核心操作是哨兵划分,目标是:选择数组中的某个元素作为“基准数”,将所有小于基准数的元素移到其左侧,大于基准数的元素移到其右侧
def partition(self,nums:list[int],left:int,right:int)->int:
# 以nums[left]为基准数
i,j=left,right
while i<j:
# 从右到左寻找首个小于基准数的元素
while i<j and nums[j]>=nums[left]:
j-=1
# 从左向右寻找首个大于基准数的元素
while i<j and nums[i]<=nums[left]:
i+=1
# 元素交换
nums[i],nums[j]=nums[j],nums[i]
# 基准数交换到两子数组的分界线
nums[i],nums[left]=nums[left],nums[i]
return i # 返回基准数的索引
def quick_sort(self,nums:list[int],left:int,right:int):
# 子数组长度为1时终止递归
if left>=right:
return
# 哨兵划分
privot=self.partition(nums,left,right)
self.quick_sort(nums,left,privot-1)
self.quick_sort(nums,privot+1,right)特性
时间复杂度
O(nlogn)、自适应性排序空间复杂度
O(n)、原地排序非稳定性排序
基准数优化
快速排序在某些输入下的时间效率可能降低。
极端例子,输入数组完全倒序,选择最左端元素作为基准数,在哨兵划分后,基准数被交换到最右端,导致左子数组长度为 n-1,右子数组长度为 0,这样递归,每轮哨兵划分都有一个子数组长度为 0,分治策略失效,退化为“冒泡排序”的近似形式
可以优化哨兵划分中的基准数的选取策略
1、随机选取一个元素,但运气不好,每次都选到不理想的基准数,效率依旧不高;
2、在数组中选取三个候选元素(通常是数组的首、尾、中点元素),并将这三个候选元素的中位数作为基准数。
"""选取三个候选元素的中位数"""
def media_three(self,nums:list[int],left:int,mid:int,right:int)->int:
l,m,r=nums[left],nums[mid],nums[right]
if (l<=m<=r) or (r<=m<=l):
return mid # m在l,r之间
if (m<=l<=r) or (r<=l<=m):
return left # l在m,r之间
return right
def partition(self,nums:list[int],left:int,right:int)->int:
med=self.media_three(nums,left,(left+right)//2,right)
# 中位数交换到数组最左端
nums[left],nums[med]=nums[med],nums[left]
i,j=left,right
while i<j:
while i<j and nums[j]>=nums[left]:
j-=1
while i<j and nums[i]<=nums[left]:
i+=1
nums[i],nums[j]=nums[j],nums[i]
nums[i],nums[left]=nums[left],nums[i]
return i尾递归优化
在某些情况下,快速排序可能占用空间较多
比如对于完全有序的输入数组,递归中的子数组长度为 m,每轮哨兵划分操作都将产生长度为 0 的左子数组和长度为 m-1 的右子数组,意味着每一层递归调用减少的问题规模非常小(只减少一个元素),递归树的高度会达到 n-1,此时需要占用O(n)大小的栈帧空间
为了防止栈帧空间的累积,可以在每轮哨兵排序完成后,比较两个子数组的长度,仅对较短的子数组进行递归。较短数组的长度不会超过n/2,因此可以确保递归深度不超过logn,从而将最差空间复杂度优化至O(n)
def quick_sort(self,nums:list[int],left:int,right:int):
while left<right:
privot=selft.partition(nums,left,right)
# 对两个子数组中较短的那个执行快速排序
if privot - left < right - privot:
# 递归排序左子数组
self.quick_sort(nums,left,privot-1)
left=privot+1 # 剩余未排序区间[privot+1,right]
else:
# 递归排序右子数组
self.quick_sort(nums,privot+1,right)
right=privot-1 # 剩余未排序数组[left,privot-1]归并排序
是一种基于分治策略的排序算法
包含划分和合并阶段:
1、划分阶段:通过递归不断地将数组从中点处分开,将长数组的排序问题转换为短数组的排序问题;
2、合并阶段:当子数组的长度为 1 时终止划分,开始合并,持续地将左右两个较短的有序数组合并为一个较长的有序数组,直至结束
def merge(nums:list[int],left:int,mid:int,right:int):
# 左子区间[left,mid],右子区间[mid+1,right]
# 创建临时数组 tmp,用于存放合并后的结果
tmp=[0]*(right-left+1)
# 初始化左子数组和右子数组的起始索引
i,j,k=left,mid+1,0
# 左右都有元素,比较,将较小元素复制到临时数组中
while i<=mid and j<=right:
if nums[i]<=nums[j]:
tmp[k]=nums[i]
i+=1
else:
tmp[k]=nums[i]
j+=1
k+=1
# 将左右子数组的剩余元素复制到临时数组中
while i<=mid:
tmp[k]=nums[j]
i+=1
k+=1
while j<=right:
tmp[k]=nums[j]
j+=1
k+=1
# 把临时数组tmp中的元素复制回原数组nums的对应区间
for k in range(0,len(tmp)):
nums[left+k]=tmp[k]
def merge_sort(nums:list[int],left:int,right:int):
# 终止条件
if left>=right:
return
# 划分阶段
mid=(left+right)//2
merge_sort(nums,left,mid) # 递归左子数组
merge_sort(nums,mid+1,right) # 递归右子数组
# 合并阶段
merge(nums,left,mid,right)特性
时间复杂度
O(nlogn)、非自适应排序空间复杂度
O(n)、非原地排序稳定排序
链表排序
对应链表,归并排序相较于其他排序算法具有显著优势,可以将链表排序任务的控制复杂度优化至O(1)
堆排序
堆
堆 heap 是一种满足特定条件的完全二叉树,主要可分为两种类型
小顶堆 min heap:任意节点的值小于等于子节点的值。
大顶堆 max heap:任意节点的值大于等于子节点的值。
特性:
最底层节点靠左填充,其他层的节点都被填满
二叉树的根节点称为“堆顶”,底层最靠右的节点称为“堆底”
大顶堆,堆顶元素最大;小顶堆,堆顶元素最小
堆的常用操作
堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列
使用角度来看,可以将“优先队列”和“堆”看作等价的数据结构
常用操作:
入堆
堆顶元素出堆
访问堆顶元素
获取堆的元素数量
判断堆是否为空
# python的heapq模块默认实现小顶堆
# 考虑将“元素取负”后再入堆,这样就可以将大小关系颠倒,从而实现大顶堆
# 初始化小顶堆
min_heap, flag = [], 1
# 初始化大顶堆
max_heap, flag = [], -1
# 元素入堆
heapq.heappush(max_heap, flag * 1)
heapq.heappush(max_heap, flag * 3)
heapq.heappush(max_heap, flag * 2)
heapq.heappush(max_heap, flag * 5)
heapq.heappush(max_heap, flag * 4)
# 获取堆顶元素
peek: int = flag * max_heap[0] # 5
# 堆顶元素出堆
# 出堆元素会形成一个从大到小的序列
val = flag * heapq.heappop(max_heap) # 5
val = flag * heapq.heappop(max_heap) # 4
val = flag * heapq.heappop(max_heap) # 3
val = flag * heapq.heappop(max_heap) # 2
val = flag * heapq.heappop(max_heap) # 1
# 获取堆大小
size: int = len(max_heap)
# 判断堆是否为空
is_empty: bool = not max_heap
# 输入列表并建堆
min_heap: list[int] = [1, 3, 2, 5, 4]
heapq.heapify(min_heap)堆的实现——大顶堆
存储:堆是一种完全二叉树,完全二叉树非常适合用数组来表示
使用数组表示二叉树时,元素代表节点值,索引代表节点在二叉树中的位置,节点指针通过索引映射公式来实现
给定索引 i,左子节点2i+1,右子节点2i+2
def left(self,i:int)->int:
return 2 * i + 1
def right(self,i:int)->int:
return 2 * i + 2
def parent(self,i:int)->int:
return (i-1)//2
# 访问堆顶
def peek(self)->int:
return self.max_heap[0]
# 元素入堆,先添加到堆底
# 堆的成立条件可能被破坏,需要修复从插入节点到根节点的路径上的各个节点
# 称为堆化heapify
def push(self,val:int):
self.max_heap.append(val)
# 从底至顶堆化
self.sift_up(self.size()-1)
def sift_up(self,i:int):
# 从节点i开始堆化
while True:
p=self.parent(i)
if p<0 or self.max_heap[i] <= self.max_heap[p]:
break
self.swap(i,p)
i=p
# 堆顶元素出堆
# 交换堆顶元素与堆底元素
# 交换之后,删除堆底,然后从根节点,从顶至底执行堆化
def pop(self)->int:
if self.is_empty():
raise IndexError("堆为空")
self.swap(0,self.size()-1)
val=self.max_heap.pop()
# 从顶至底堆化
self.sift_down(0)
return val
def sift_down(self,i:int):
while True:
l,r,ma=self.left(i),self.right(i),i
if l<self.size() and self.max_heap[l]>self.max_heap[ma]:
ma=l
if r<self.size() and self.max_heap[r]>self.max_heap[ma]:
ma=r
if ma==i:
break
self.swap(i,ma)
# 循环向下堆化
i=ma堆排序
基于堆数据结构实现的高效排序算法
可以利用已经“建堆操作”和“元素出堆操作”实现堆排序:
1、输入数组并建立小顶堆,此时最小元素位于堆顶
2、不断执行出堆操作,依次记录出堆位置,即可得到从小到大排序的序列
def heap_sort(nums:list[int]):
for i in range(len(nums)//2 - 1 , -1, -1):
sift_down(nums,len(nums),i)
for i in range(len(nums) - 1, 0, -1):
nums[0],nums[i]=nums[i],nums[0]
sift_down(nums,i,0)特性
时间复杂度
O(nlogn)、非自适应排序空间复杂度
O(1)、原地排序非稳定性排序
桶排序
桶排序 bucket sort 是分治策略的一个典型应用。
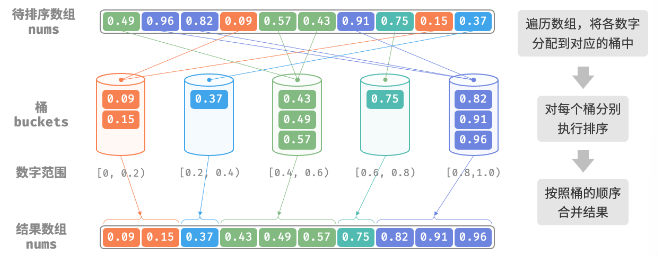
通过设置一些具有大小顺序的桶,每个桶对应一个数据范围,将数据平均分配到各个桶中;然后,在每个桶内部分别执行排序;最终按照桶的顺序将所有数据合并
算法流程
考虑一个长度为 n 的数组,其元素范围是[0,1)内的浮点数。
1、初始化 k 个桶,将 n 个元素分配到 k 个桶中
2、对每个桶分别执行排序
3、按照桶从小到大的顺序合并结果
def bucket_sort(nums:list[float]):
# 初始化k=n/2个桶,预期向每个桶分配2个元素
buckets=[[] for _ in range(k)]
# 将元素分配到各个桶中
for num in nums:
# 输入的数据范围是[0,1),使用num*k映射到索引范围[0,k-1]
i=int(num*k)
# 将num添加到桶i
buckets[i].append(num)
# 对各个桶执行排序
for bucket in buckets:
bucket.sort()
# 遍历合并结果
i=0
for bucket in buckets:
for num in bucket:
nums[i]=num
i+=1特性
桶排序适用于处理体量很大的数据。
例如,输入 100 万个元素,由于空间限制,系统内存无法一次性加载所有数据。此时可以将数据分为 1000 个桶,然后分别对每个桶进行排序,最后将结果合并。
时间复杂度为
O(n+k):假设元素在各个桶内平均分布,那么每个桶内的元素数量为n/k,假设排序单个桶使用O(n/k log n/k),则排序所有桶使用O(n log n/k),当桶数量 k 比较大时,时间复杂度趋于O(n),合并结果时需要遍历所有桶和元素,花费O(n+k)时间自适应排序
空间复杂度为
O(n+k)、非原地排序
如何平均分配
桶排序的时间复杂度理论上可以达到 O(n),关键在于将元素均匀分配到各个桶中,因为实际数据往往不是均匀分配的。
为实现平均分配,可以预先设定一条大致的分界线,将数据粗略地分到 3 个桶中。
分配完毕后,再将商品较多的桶继续划分为 3 个桶,直至所有桶中的元素数量大致相等。
如果提前知道数据的概率分布,可以根据数据概率分布设置每个桶的分界线
计数排序
通过统计元素数量来实现排序,通常应用于整数数组
流程
给定一个长度为 n 的数组 nums,其中的元素都是非负整数
1、遍历数组,找出其中的最大数字,记为 m,然后创建一个长度为m+1的辅助数组 counter
2、借助 counter 统计 nums 中各数字的出现次数,其中counter[num]对应数字 num 的出现次数。统计的方法,只需要遍历 nums
3、遍历 counter,根据各数字出现次数从小到大顺序填入 nums
def counting_sort_naive(nums:list[int]):
# 统计数字最大元素m
m=0
for num in nums:
m=max(m,num)
counter=[0]*(m+1)
for num in nums:
counter[num]+=1
i=0
for num in range(m+1):
for _ in range(counter[num]):
nums[i]=num
i+=1完整实现
如果输入数据是对象,按照对象的某一属性排序, 就无法按照上述步骤还原数组
此时可以先计算 counter 的前缀和,索引 i 的前缀和prefix[i]等于数组前 i 个元素之和
prefix[num]-1代表元素 num 在结果数组 res 中最后一次出现的索引
这样可以知道各个元素应该出现在结果数组的哪个位置
然后就可以倒序遍历原数组 nums 的每个元素 num,在每轮迭代中执行:
1、将 num 填入数组 res 的索引prefix[num]-1处
2、令前缀和prefix[num]减小 1,从而得到下次放置 num 的索引
def counting_sort(nums: list[int]):
"""计数排序"""
# 完整实现,可排序对象,并且是稳定排序
# 1. 统计数组最大元素 m
m = max(nums)
# 2. 统计各数字的出现次数
# counter[num] 代表 num 的出现次数
counter = [0] * (m + 1)
for num in nums:
counter[num] += 1
# 3. 求 counter 的前缀和,将“出现次数”转换为“尾索引”
# 即 counter[num]-1 是 num 在 res 中最后一次出现的索引
for i in range(m):
counter[i + 1] += counter[i]
# 4. 倒序遍历 nums ,将各元素填入结果数组 res
# 初始化数组 res 用于记录结果
n = len(nums)
res = [0] * n
for i in range(n - 1, -1, -1):
num = nums[i]
res[counter[num] - 1] = num # 将 num 放置到对应索引处
counter[num] -= 1 # 令前缀和自减 1 ,得到下次放置 num 的索引
# 使用结果数组 res 覆盖原数组 nums
for i in range(n):
nums[i] = res[i]特性
时间复杂度为
O(n+m)、非自适应排序空间复杂度为
O(n+m)、非原地排序稳定排序
局限性
1、计数排序只适用于非负整数
2、计数排序适用于数据量大但数据范围较小的情况
基数排序
核心思想与计数排序一致,也通过统计个数来实现排序。在此基础上,基数排序利用数字各位之间的递进关系,依次对每一位进行排序,从而得到最终的排序结果。
流程
1、初始化位数 k=1
2、对第 k 位执行计数排序。完成后,数据根据第 k 位从小到大排序
3、将 k 增加 1,然后返回步骤 2,继续迭代,直到所有位都排序完成后结束

def digit(num:int,exp:int)->int:
"""获取元素num的第k位,其中exp=10^(k-1)"""
return (num//exp)%10
def counting_sort_digit(nums:list[int],exp:int):
"""根据nums第k位排序"""
# 十进制的位范围为0~9,因此需要长度为10的桶数组
counter=[0]*10
n=len(nums)
# 统计0~9的出现次数
for i in range(n):
d=digit(nums[i],exp)
counter[d]+=1
# 求前缀和,将出现个数转换为数组索引
for i in range(1,10):
counter[i]+=counter[i-1]
# 倒序遍历,根据桶内统计结果,将各元素填入res
res=[0]*n
for i in range(n-1,-1,-1):
#
d=digit(nums[i],exp)
# 获取d在数组中的索引
j=counter[d]-1
# 将当前元素填入索引j
res[j]=nums[i]
# 将d的数量减1
counter[d]-=1
# 使用结果覆盖原数组nums
for i in range(n):
nums[i]=res[i]
def radix_sort(nums:list[int]):
m=max(nums)
exp=1
while exp<=m:
# 对数组元素的第k位执行计数排序
# k=1 -> exp=1
# k=2 -> exp=19
# 即 exp=10^(k-1)
counting_sort_digit(nums,exp)
exp*=10特性
基数排序适用于数值范围较大的情况,但前提是数据必须可以表示为固定位数的格式,且位数不能过大
时间复杂度
O(nk)、非自适应排序空间复杂度
O(n+d)、非原地排序稳定排序
最高位优先 Most Significant Digit first 法
MSD:从左往右
最低位优先 Least Significant Digit first 法
LSD:从右往左
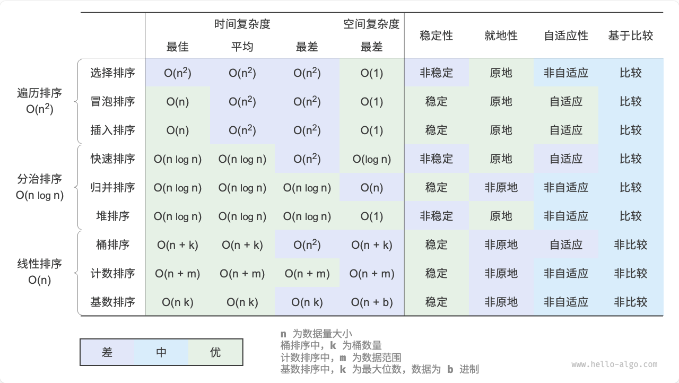
总结
参考
https://www.hello-algo.com/chapter_sorting/sorting_algorithm/
