精度问题
精度问题
JavaScript 中 Number 采用的是 IEEE754 规范中 64 位双精度浮点数编码
这样的储存结构优点是可以归一化处理整数和小数,节省存储空间
对于整数,可以轻易转化成十进制或者二进制,但对于浮点数,因为小数点的存在,小数点的位置不是固定的,解决方法是使用科学计数法
但计算机只能使用二进制表示,二进制转换为科学计数法的公式为:x=a*2^e
存储二进制时小数点的偏移量最大为 52 位,最多可以表达的位数是2^53,对应科学计数的尾数是9.007199254740992,这是 JS 最多能表示的精度
长度是 16,所以可以使用 toPrecision(16)来做精度运算,超过的精度会自动做凑整处理
为什么会有精度问题?
在计算机中,某些十进制的数字不能用有限的二进制位数精确表示。例如,0.1 和 0.2 在二进制中无法精确表示,它们会被近似为某个二进制浮点数。这种近似表示会导致运算结果不完全准确。
常见的精度问题
1、浮点数相加
console.log(0.1 + 0.2); // 输出 0.300000000000000042、减法问题
console.log(0.3 - 0.1); // 输出 0.199999999999999983、乘法问题
console.log(0.1 * 0.2); // 输出 0.020000000000000004js 处理精度问题
toFixed()方法四舍五入
toFixed() 方法可以将数字四舍五入到指定的小数位数:
console.log((0.1 + 0.2).toFixed(2)); // 输出 "0.30"使用 toPrecision() 控制总的有效位数
toPrecision() 可以将数字格式化为指定的总位数
console.log((0.1 + 0.2).toPrecision(2)); // 输出 "0.30"避免使用浮点数,转换为整数进行计算
通过将浮点数乘以一个合适的倍数,转换成整数进行计算,可以有效避免精度问题,最后再除以相应的倍数还原结果
console.log((0.1 * 10 + 0.2 * 10) / 10); // 输出 0.3
console.log((0.3 * 100 - 0.1 * 100) / 100); // 输出 0.2使用 Math.round() 进行四舍五入
console.log(Math.round((0.1 + 0.2) * 100) / 100); // 输出 0.3使用大数库(BigNumber)进行精确计算
JavaScript 本身的 Number 类型有精度限制,但可以使用一些外部的库来解决精度问题。常见的库包括:
Big.js:用于精确处理小数的运算。
bignumber.js:可以处理非常大的数字和精确的小数运算。
decimal.js:可以处理小数运算的高精度库。
JavaScript 内置的 BigInt 类型(适用于整数运算)
const bigInt1 = BigInt(9007199254740991);
const bigInt2 = BigInt(1);
console.log(bigInt1 + bigInt2); // 输出 "9007199254740992n"使用 ES2020 的 Number.EPSILON
Number.EPSILON 是 JavaScript 中最小的浮点误差值,可以用来判断两个浮点数是否“足够接近”,即它们的差值是否小于 Number.EPSILON。
function isEqual(a, b) {
return Math.abs(a - b) < Number.EPSILON;
}
console.log(isEqual(0.1 + 0.2, 0.3)); // 输出 true数字在计算机中的表示
原码、反码和补码
1、原码
是一种直观的表示方法,直接使用最高位作为符号位,剩下的位表示数值的大小,符号位为 0 表示正数,-1 表示负数
示例:
例子(以8位为例):
+5 的原码表示:00000101
-5 的原码表示:10000101优点:表示方式直观,容易理解
缺点:加减法运算比较复杂,需要专门处理符号位
2、反码
是一种对负数进行特殊表示的方法,是将正数的二进制位取反得到的。正数的反码和原码相同,而负数的反码通过将对应正数的原码逐位取反(0 变 1,1 变 0)得到
特点:
正数的反码和原码相同
负数的反码是对应正数原码的二进制码诸位取反
例子:
+5 的反码:00000101(和原码相同)
-5 的反码:对 +5 的二进制取反,得到 11111010优点:
加法运算稍有简化,反码在一些早期计算机中用于简化硬件设计
缺点:
和原码一样,存在两个零的表示:+0 表示为 00000000,-0 表示为 11111111,这仍然会带来不必要的复杂性
加减法运算仍然不是最优,需要处理进位和借位的复杂情况
3、补码
补码是现代计算机系统中最常用的负数表示方法。它解决了原码和反码的一些不足,使得加减法可以统一处理,简化了硬件设计。补码的负数表示通过取反加一来获得,即:负数的补码是对应正数的反码再加 1。
特点:
正数的补码和原码相同
负数的补码是正数的反码加 1
只有一种零表示
例子:
+5 的补码:00000101(和原码、反码相同
-5 的补码:对 +5 取反得到 11111010,然后加 1,得到 11111011优点:
唯一的零
加减法统一处理
硬件简单:硬件设计更简单,减少了复杂的处理逻辑
总结
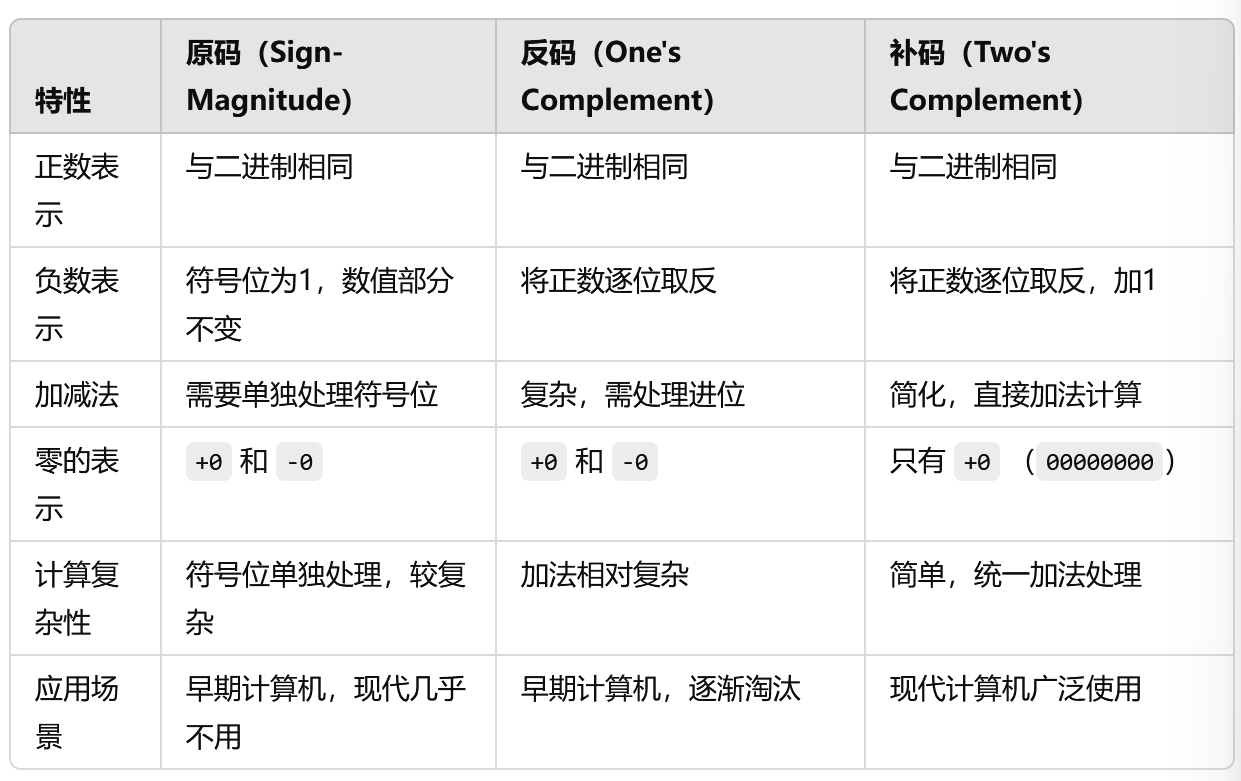
8 位情况下:
整数的表示
无符号整数
无符号整数只表示非负数,没有符号位
一个 n 位的无符号整数可以表示的范围是 0 到 2^n - 1
有符号整数
有符号整数可以表示正数和负数。通常采用补码(Two's Complement)方式来表示有符号整数。在 n 位系统中,第一个位(最高位)是符号位,用于表示正负
浮点数表示
浮点数表示的是带有小数部分的数。由于计算机中小数的表示和处理较为复杂,通常采用IEEE 754 标准来表示浮点数
浮点数表示由三部分组成:
1、符号位
2、指数:用来表述数的范围
3、尾数:表示有效数字
单精度浮点数(32位,float)
在单精度浮点数中,32 位被分配如下:
1 位:符号位。
8 位:指数位,存储的是指数的偏移值(偏移127)。
23 位:尾数位,用于表示有效位数。
双精度浮点数(64位,double)
在双精度浮点数中,64 位被分配如下:
1 位:符号位。
11 位:指数位,存储的是指数的偏移值(偏移1023)。
52 位:尾数位,用于表示有效位数。
IEEE 754标准的表示方法
浮点数的值由以下公式计算:
(-1)^符号位 × 尾数 × 2^指数偏移大整数
为了处理非常大的整数,JavaScript引入了 BigInt 类型,它能够表示任意大小的整数,而不像普通的 Number 类型那样有固定的大小限制
BigInt 的特性:
BigInt 不会出现 Number 类型的精度丢失问题。
通过在整数末尾加上 n 来创建 BigInt 值
const bigInt = 1234567890123456789012345678901234567890n;其他特殊数字的表示
NaN
NaN 是 JavaScript 中表示非数字值的一个特殊数值
通常在无效的数学操作(如 0/0)中产生
console.log(1 / 0); // 输出 Infinity
console.log(-1 / 0); // 输出 -InfinityInfinity(正无穷大)和 -Infinity(负无穷大)
当计算结果超出了可表示的范围时,JavaScript会返回 Infinity 或 -Infinity
console.log(1 / 0); // 输出 Infinity
console.log(-1 / 0); // 输出 -Infinity定点数的表示
定点数(Fixed-point number)是一种表示小数的方式,尤其是在某些嵌入式系统中使用。定点数通过将小数部分放大为整数来表示。常见的做法是将所有小数乘以一个固定的倍数(如 100、1000),然后使用整数进行计算。定点数的计算比浮点数更高效,但灵活性较低,无法表示非常大或非常小的数。
BCD(Binary-Coded Decimal)表示法
BCD(二进制编码十进制) 是一种将十进制数用4位二进制编码表示的方法。每个十进制数的每一位用4位二进制表示,因此在处理需要精确表示的场景(如金融数据)时,BCD比浮点数更精确
字符编码与数字表示
在计算机中,数字有时也以字符形式存储。常见的字符编码如 ASCII、Unicode 规定了数字字符如何表示。例如,字符 '1' 在 ASCII 编码中表示为 49(十进制),在二进制中为 00110001。
